1단계.
B진법 수 N이 주어진다. 이 수를 10진법으로 바꿔 출력하는 프로그램을 작성하시오.
10진법을 넘어가는 진법은 숫자로 표시할 수 없는 자리가 있다. 이런 경우에는 다음과 같이 알파벳 대문자를 사용한다.
A: 10, B: 11, ..., F: 15, ..., Y: 34, Z: 35
첫째 줄에 N과 B가 주어진다.
첫째 줄에 B진법 수 N을 10진법으로 출력한다.
답: n,b=input().split()
print(int(n,int(b)))
n과 b를 문자열로 입력받는다.
int(n, int(b))는 문자열 n을 b 진수로 해석하여 10진수로 변환하는 코드다. 예를 들어 '1010 2'를 입력하면 n='1010', b='2'
1010을 2진수로 해석하여 10진수로 변환하고 출력하게 된다. (결과: 10) 파이썬이어서 코드가 간결하게 나온다. (파이썬에 내장된 N차 진수를 10진수로 변환하는 코드)
2단계.
10진법 수 N이 주어진다. 이 수를 B진법으로 바꿔 출력하는 프로그램을 작성하시오.
10진법을 넘어가는 진법은 숫자로 표시할 수 없는 자리가 있다. 이런 경우에는 다음과 같이 알파벳 대문자를 사용한다.
A: 10, B: 11, ..., F: 15, ..., Y: 34, Z: 35
첫째 줄에 N과 B가 주어진다.
첫째 줄에 10진법 수 N을 B진법으로 출력한다.
답: list = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ"
n, b = map(int, input().split())
answer = ""
while (n != 0):
answer = list[n % b] + answer
n //= b
print(answer)
첫 번째 문제와 이번 두 번째 문제는 비슷한 구석이 있다. 단지 첫 번째 문제는 파이썬 내부 코드로 간단하게 구현이 가능할 뿐이다. (두 번째는 따로 없다...)
먼저 진법을 표기할 list를 정의한다. (0부터 z까지) 이후 n과 b를 숫자로 기입받는다. 최종 출력은 answer이다.
이후 n이 0이 아닐 동안 while문을 돌린다. 진법을 바꾸는 것은 나눗셈과 관련이 있다. list를 배열처럼 여기고, n을 b로 나눈 나머지를 answer에 기입해 준다. (초기화 값은 공백 < 아무것도 없는 문자열) 이후 n을 b로 나눈 몫을 다시 n에 넣어준다.
이 과정을 반복하다 보면 n이 0이 되는 순간이 온다. (진법 범위는 2진수부터 36진수까지)
3단계.
거스름돈의 액수가 주어지면 리암이 줘야 할 쿼터(Quarter, $0.25)의 개수, 다임(Dime, $0.10)의 개수, 니켈(Nickel, $
0.05)의 개수, 페니(Penny, $0.01)의 개수를 구하는 프로그램을 작성하시오. 거스름돈은 항상 $5.00 이하이고, 손님이 받는 동전의 개수를 최소로 하려고 한다. 예를 들어, $1.24를 거슬러 주어야 한다면, 손님은 4 쿼터, 2 다임, 0 니켈, 4 페니를 받게 된다.
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 거스름돈 C를 나타내는 정수 하나로 이루어져 있다. C의 단위는 센트이다. (1달러 = 100센트)
각 테스트케이스에 대해 필요한 쿼터의 개수, 다임의 개수, 니켈의 개수, 페니의 개수를 공백으로 구분하여 출력한다.
답: list = [25, 10, 5, 1] #쿼터 다임 니켈 페니
T = int(input())
for a in range(T) :
C = int(input())
rest = []
for i in list :
rest.append(C // i) # 몫이 개수가 됨
C = C % i # 나머지는 다시 C에 저장
print(*rest) # 한 줄 출력
미리 쿼터 다임 니켈 페니의 개수를 list 배열로 정의해 둔다. 이후 T를 기입받아 준다. 그다음 for문을 T만큼 돌려준다. 거스름돈도 받아야 하니 C도 입력받아준다. 실제로 출력할 부분은 rest로 정의한다.
이후 list의 값을 순차적으로 처리한다. rest 배열에 C를 i로 나눈 만큼 추가해 준다. 나머지는 다시 C에 저장한다.
*rest는 rest의 배열을 공백을 주어 한 줄로 출력하게 만든다.
4단계.
알고리즘을 시작하면서 상근이는 정사각형을 이루는 점 4개를 고른다. 그 후에는 다음과 같은 과정을 거쳐서 지형을 만든다.
정사각형의 각 변의 중앙에 점을 하나 추가한다. 정사각형의 중심에 점을 하나 추가한다.
초기 상태에서 위와 같은 과정을 한 번 거치면 총 4개의 정사각형이 새로 생긴다. 이와 같은 과정을 상근이가 만족할 때까지 계속한다.
상근이는 어떤 점은 한 개 보다 많은 정사각형에 포함될 수 있다는 사실을 알았다. 메모리 소모량을 줄이기 위해서 중복하는 점을 한 번만 저장하려고 한다. 과정을 N번 거친 후 점 몇 개를 저장해야 하는지 구하는 프로그램을 작성하시오.
첫째 줄에 N이 주어진다. 첫째 줄에 과정을 N번 거친 후 점의 수를 출력한다.

답: N = int(input())
print((2**N+1)**2)
코드는 단순해 보인다. 그러나 "중앙 이동 알고리즘"이 들어가 있는 코드이다. 과정을 모르면 바로 생각하기 힘든 코드. (구글링 하고 나서야 알았다..)
0번일 때에는 점이 4개다. 1번 할 때에는 점이 9개다. 2번 할 때에는 점이 25개이다... 잘 보면 제곱수이라는 힌트를 알아챌 수 있다. (5번 할 때에는 점이 1089개이고 이건 33의 제곱이다.)
잘 보면 홀수의 제곱이다. 다만 0번일 때에는 점이 짝수이다. 이건 홀수를 표현할 때 2 ** N + 1 ~~ 로 표현해야 함을 뜻한다.
이 논리를 적용하면 다음과 같을 것이다.
1. N이 0이라면? 2의 0 제곱이다. 그러면 1이 나온다. 이후 1 + 1 = 2이고, 2를 제곱하면 4가 나온다.
2. N이 1이라면? 2의 1 제곱이다. 그러면 2가 나온다. 이후 2 + 1 = 3이고, 3을 제곱하면 9가 나온다.
....
따라서 연산에 대한 알고리즘은 ((2의 N제곱 + 1)의 2 제곱)이라고 생각할 수 있다.
5단계.
위의 그림과 같이 육각형으로 이루어진 벌집이 있다. 그림에서 보는 바와 같이 중앙의 방 1부터 시작해서 이웃하는 방에 돌아가면서 1씩 증가하는 번호를 주소로 매길 수 있다. 숫자 N이 주어졌을 때, 벌집의 중앙 1에서 N번 방까지 최소 개수의 방을 지나서 갈 때 몇 개의 방을 지나가는지(시작과 끝을 포함하여)를 계산하는 프로그램을 작성하시오. 예를 들면, 13까지는 3개, 58까지는 5개를 지난다.
입력으로 주어진 방까지 최소 개수의 방을 지나서 갈 때 몇 개의 방을 지나는지 출력한다.

답: n = int(input())
numbox = 1
cnt = 1
while (n > numbox):
numbox += 6 * cnt
cnt += 1
print(cnt)
일명 벌집문제. 숫자가 늘어나는 규칙을 찾고 그 규칙을 코드로 작성해야 하는 문제이다. 이 문제의 전환점은 7번 타일이다. 7은 6 x 1 + 1이라고 생각할 수 있다. 19는 6 x 3 + 1 , 37은 6 x 6 + 1... 61은 6 x 10 + 1인 것이다.
그러면 1은 무엇일까? 그렇다. 6 x 0 + 1 인 것이다. 포인트는 곱하기이다. 곱하기가 0 > 1 > 3 > 6 > 10... 이렇게 커진다.
스타트는 전부 1에서 시작한다. numbow도 1, 카운팅 할 cnt도 1로 초기화한다.
이후 입력을 받은 n이 numbox보다 작거나 같을 때까지 반복문이 돌아간다. 만일 n이 1이라면? 그냥 정답은 1인 것이다. (즉, 스타트 지점인 1도 카운팅 하고 들어간다.)
말이 복잡하지만, 결국 규칙성은 6의 배수로 겹집이 커진다는 것이라고 간단히 말할 수 있다.
6단계.
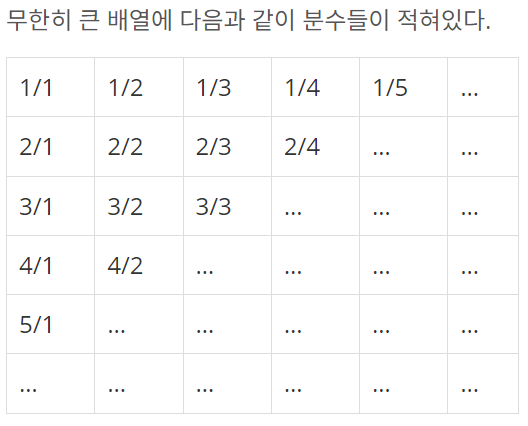
이와 같이 나열된 분수들을 1/1 → 1/2 → 2/1 → 3/1 → 2/2 → … 과 같은 지그재그 순서로 차례대로 1번, 2번, 3번, 4번, 5번, … 분수라고 하자.
X가 주어졌을 때, X번째 분수를 구하는 프로그램을 작성하시오.
답: x = int(input())
line = 1
while x > line:
x -= line
line += 1
if line%2 == 0:
a = x
b = line-x+1
else:
a = line-x+1
b = x
print(a, '/', b, sep='')
짝수번째라인은 분자가 오름차순/분모가 내림차순
홀수번째라인은 분자가 내림차순/분모가 오름차순
이 규칙을 알아내야 코드를 짤 수 있다.

빨간색을 보자. 짝수번째 라인이다(2번). 분자를 보면 2 > 1로 내려간다. 분모를 보면 1 > 2로 올라간다.
짝수번째 라인인 4번 라인을 보자. 분자를 보면 4 > 3 > 2 > 1로 내려간다. 분모를 보면 1 > 2 > 3 > 4로 올라간다. 반대로 홀수 번째는 분자가 1 > 2 > 3 > 4 > 5로 올라간다. 분모는 5 > 4 > 3 > 2 >1로 내려간다..
이제, line를 정의해 두고 이 line을 기준으로 분자 분모를 계산한다.
이때 분자는 a이며 b가 분모가 된다. (출력은 a와 b가 핵심이다)
입력받은 x가 line보다 작거나 같다면 반복문은 끝난다.
line이 짝수면 a에 x를 기입, b에는 line - x + 1을 기입해 준다. line이 홀수면 반대로 해준다.
이후 반복문이 끝나면 나오는 a와 b를 출력해 준다. (sep은 a와 b 사이에 문자열을 넣어주는 함수다.)
7단계.
달팽이는 높이가 V미터인 나무 막대를 올라갈 것이다.
달팽이는 낮에 A미터 올라갈 수 있다. 하지만, 밤에 잠을 자는 동안 B미터 미끄러진다. 또, 정상에 올라간 후에는 미끄러지지 않는다.
달팽이가 나무 막대를 모두 올라가려면, 며칠이 걸리는지 구하는 프로그램을 작성하시오.
첫째 줄에 세 정수 A, B, V가 공백으로 구분되어서 주어진다.
답: a, b, v = map(int, input().split())
day = (v - b) / (a - b)
if (day == int(day)):
print(int(day))
else :
print(int(day)+1)
이 문제의 제한시간은 0.25초. 즉 반복문을 쓰지 말라는 뜻이다. 이 부분은 시간 복잡도 문제와도 어느 정도 연관이 있다. (시간 복잡도는 따로 알고리즘으로 빼서 공부해야 할 듯)
우리가 원하는 것은 "며칠"이다. 이걸 day로 정의해 준다. 예를 들어보자. 나무 막대가 4미터가 있다. 낮에는 2미터를 올라간다. 밤에는 1미터 미끄러진다. (아, 참고로 하루는 낮과 밤으로 이루어져 있다..)
1일 차. 낮에 2미터를 올라간다. 밤에 1미터를 미끄러졌다. 현재 위치는 1미터다.
2일 차. 낮에 2미터를 올라간다. 밤에 1미터를 미끄러졌다. 현재 위치는 2미터다.
3일 차. 낮에 2미터를 올라간다. 4미터. 즉 정상에 도달했다. 고로 3일이 걸렸다.
식을 세우면 day는 총길이(v)에서 미끄러지는 길이(b)를 뺀 값에서, 올라간 길이(a)에서 미끄러지는 길이(b)를 뺀 값을 나눈 값이다. 예를 든 사례를 적용하자면 (4-1) / (2-1) = 3 인 것.
근데 문제가 있다. 1.~~ 일이라는 것은 없다는 점이다. 고로 강제 형변환이 필요한 시점이다. 만일 그냥 day와 int로 강제 형변환 값이 같다면? 그냥 그대로 강제 형변환된 day를 출력하면 된다. 그게 아니라면 강제 형변환된 day에 1을 더해줘야 한다. 왜냐하면 강제 형변환은 뒤의 소수점을 제거하는 방식이기 때문. 예를 들어서
v가 5이고 a가 4, b가 1이라면? 4 / 3이고 이건 1.3333이다. 형변환하면 1이 나온다. 근데 엄연히 1보다는 큰 값이니 1을 더해서 하루를 완성시켜야 하는 것이다. (그림을 그려보면 바로 알 수 있다.) - 포인트는 "정상에 도달하면 그걸로 끝"인 것!
오늘의 결론
수학문제는 결국 "특정 규칙"을 찾아내는 것이 관건이다.
'백준 (코테)' 카테고리의 다른 글
| 10. [10단계] 제목: 기하: 직사각형과 삼각형 (1~4챕터) (0) | 2024.08.20 |
|---|---|
| 9. [9단계] 제목: 약수, 배수와 소수 단계 (2) | 2024.08.17 |
| 7. [7단계] 제목: 2차원 배열 (0) | 2024.08.15 |
| 6. [6단계] 제목: 심화 1단계 (0) | 2024.08.14 |
| 5. [5단계] 제목: 문자열 (1) | 2024.08.13 |


